OCR Physics Combined Sciences
Motion
P2.1-1 Speed
Devices used to measure distance: tape measure, metre rule, light gates, ticker tape machine, odometer of a car, GPS
How to measure time: stopwatch, data-logger connected to light gates
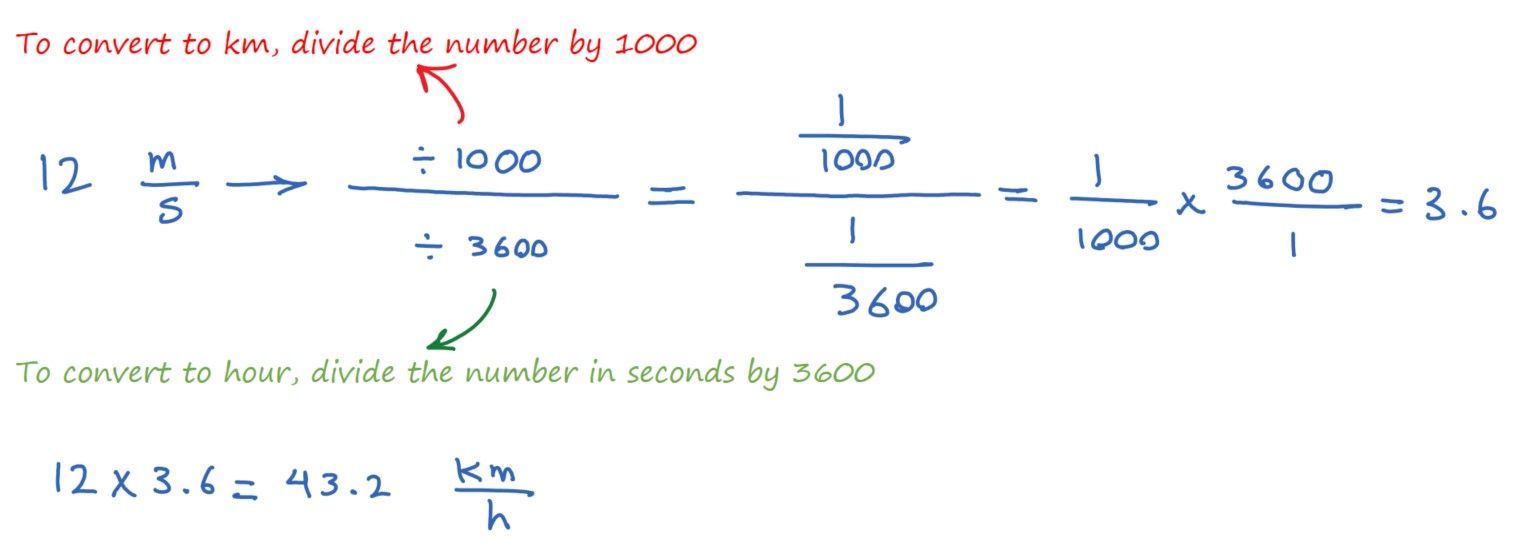
Convert units of speed:
Example 1: a car is moving with a speed of 12 m/s. calculate its speed in km/h.
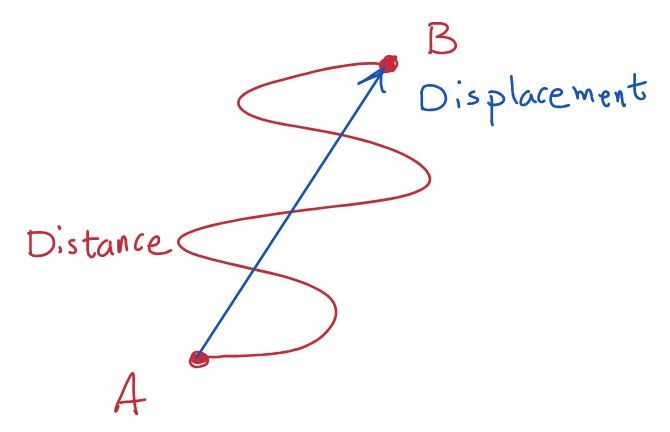
P2.1-2 Scalar and Vector:

Question 1: if you walk in a circular path of radius 5 metres, and walk for half a circle;
- What is the distance you walk?
- What is your displacement?
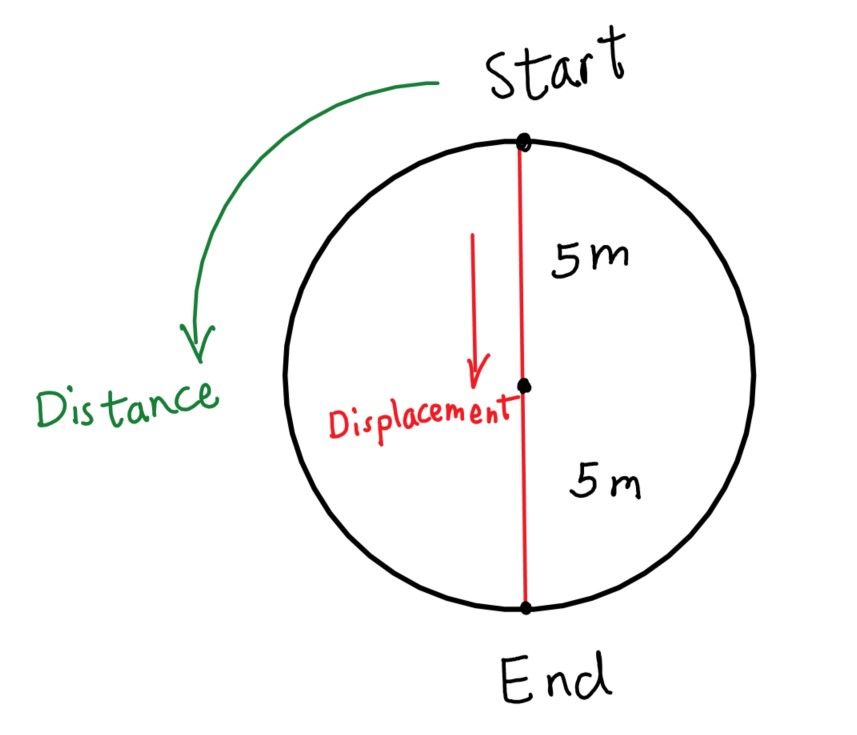
Answer:
- The distance travelled is half of the circumference of the circle: (15.7 m)
- The displacement is the diameter: 5+5 = 10 m, and we should mention the direction, for this case we can due south.
Vectors can be shown by an arrow: the size shows the magnitude, and the direction shows the direction!
P2.1-3 Distance-Time graph:
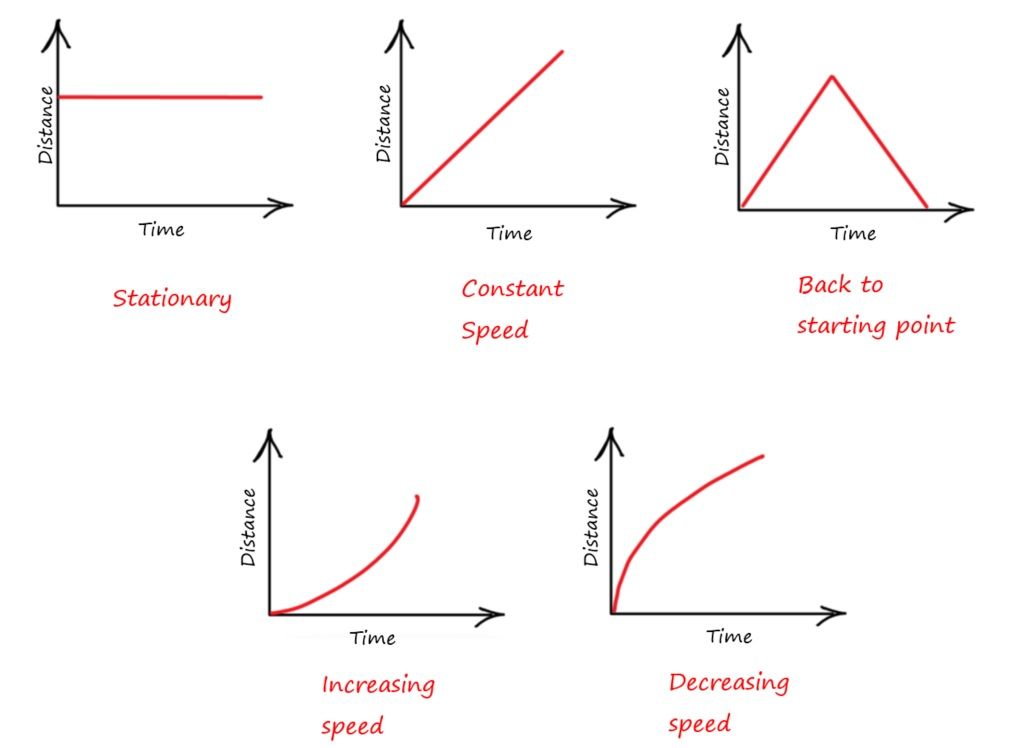
Gradient of distance-time graph shows the speed.
If the object is moving with constant speed, we have a straight line and the gradient is the rise over run or change in y over change in x (just gradient of the line! ).
If the speed is changing, graph is a curve. To find the gradient of a curve at a point, we draw a tangent to the curve at that point (point P in the figure below):
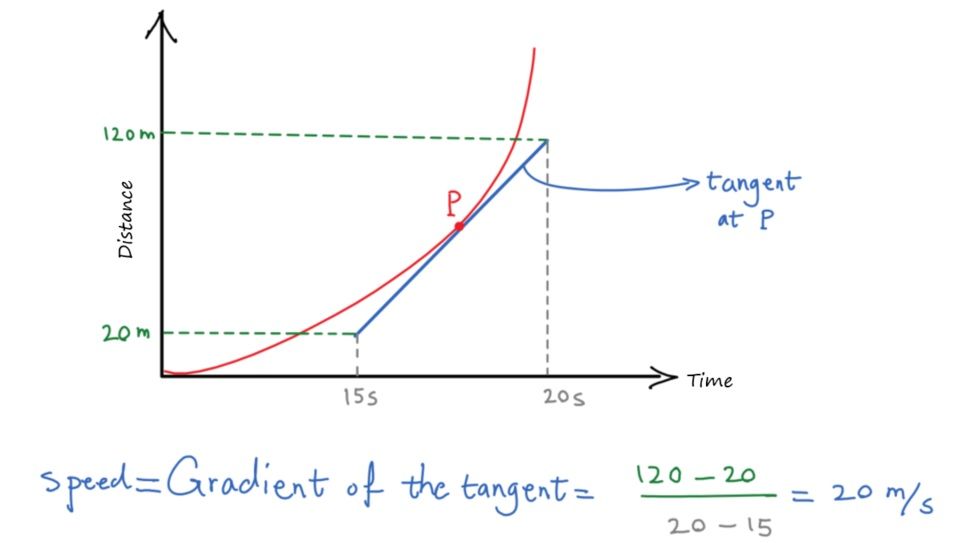
P2.1-4 Velocity-Time graph:
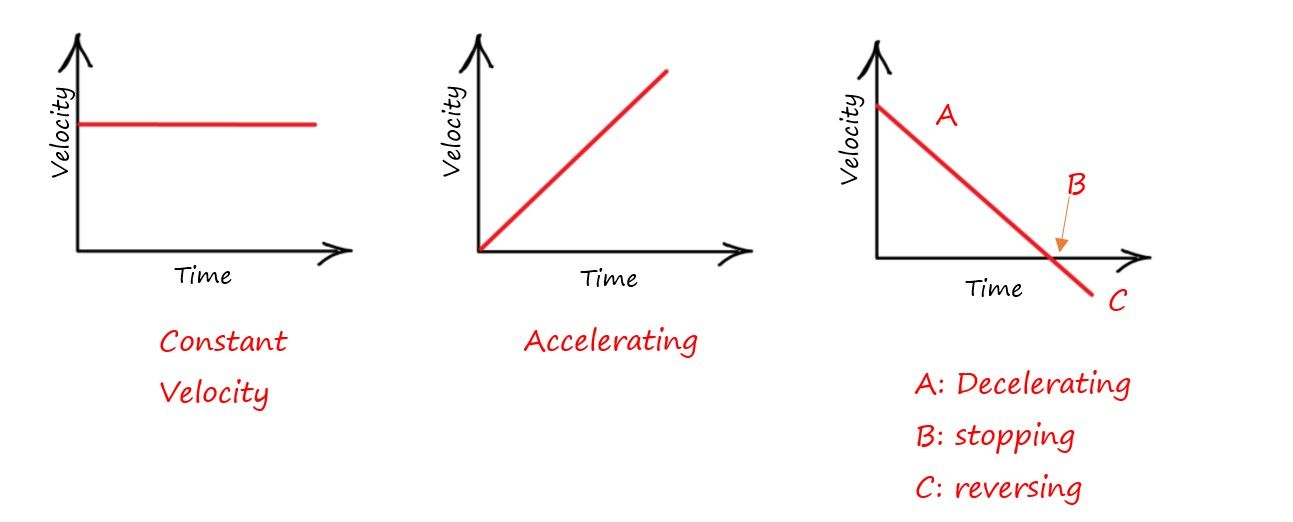
Gradient of Velocity-Time graph shows the acceleration.
Area under the Velocity-Time graph shows distance travelled.
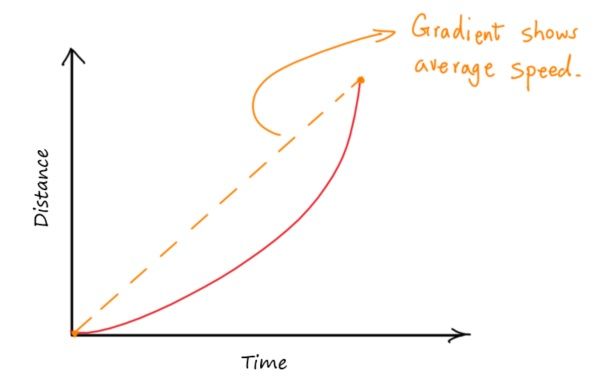
Average speed:
The average speed is total distance travelled divided by the total time, or the gradient of the line connecting the very first point of the graph to the very last point:
P2.1-5 Motion Formulae:
SUVAT Equations:
| s | Distance (m) |
| u | Initial velocity (m/s) |
| v | Final velocity (m/s) |
| a | Acceleration (m/s2) |
| t | Time (s) |
Acceleration:
Example 1:
Pedram is driving on a motorway and decreases his speed from 126 km/h to 72 km/h in 5 seconds. Find the deceleration in m/s2.
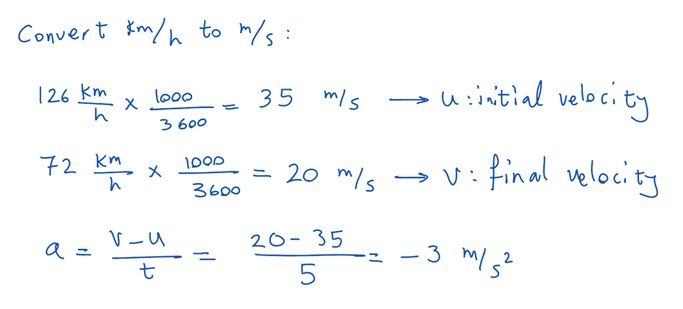
Deceleration is a negative acceleration! Because final velocity is smaller than the initial.
Timeless equation:
Example 2: an aeroplane accelerates from rest at 4.0 m/s2. Calculate how far it has travelled after 10 seconds on the runway.
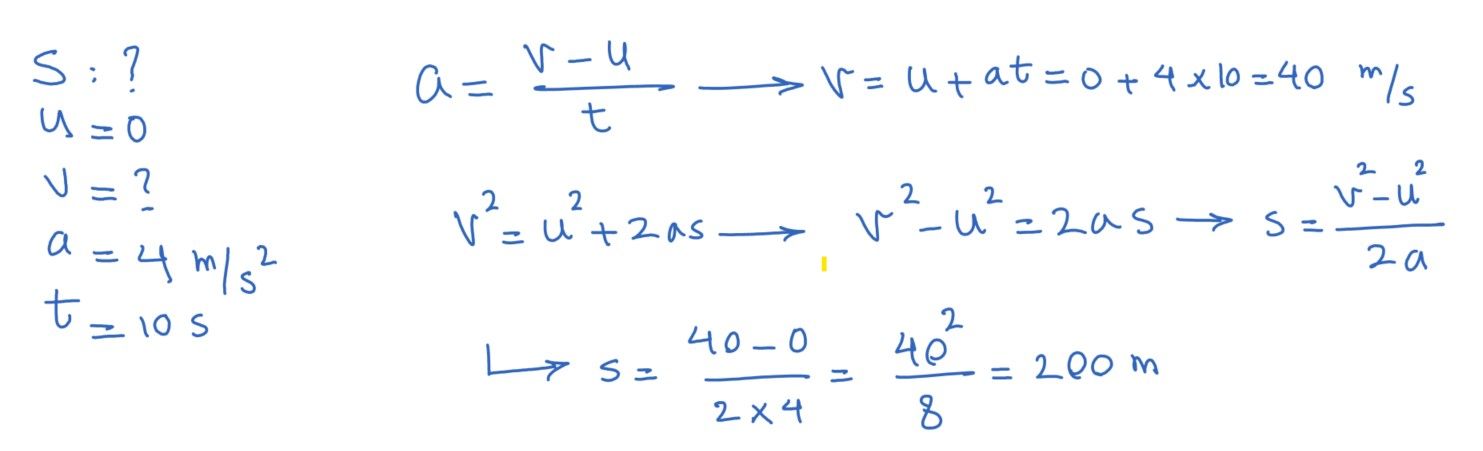
** Note: with one equation, we can only find one unknown! So in the above question, first we need to find the final velocity, otherwise we have two unknowns and one equation!
Example 3: a car is travelling at 40 as it approaches red traffic lights. It reduces its speed at a rate of 2 m/s2. Calculate how far from the stop lights should the car brake to be able to stop just at the lights.
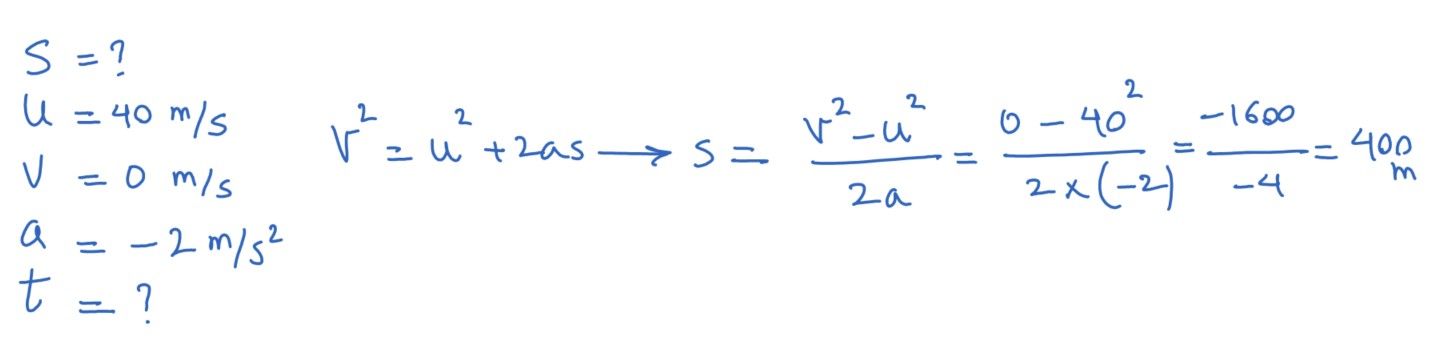
Free Fall:
All objects falling towards the earth under gravity have an acceleration of about 10 m/s2 (more precisely 9.81 m.s2). If you throw something upwards it will decelerate with -10 m/s2.
Question 4: a boy throws an apple upwards with a speed of 10 m/s. calculate the maximum height the apple will reach. Ignore air resistance.
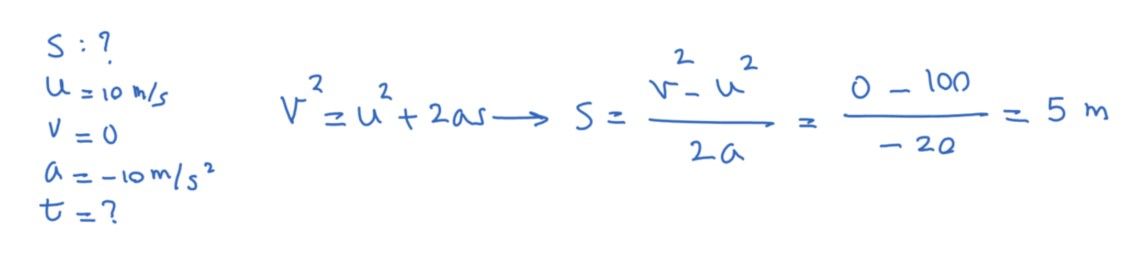
**Note: the apple will stop for just moment when it reaches maximum height. So v = 0 m/s.
Some numbers you should know:
0 – 100 km/h for a car about 6 seconds
Typical adult sprints 100 m in about 15 seconds.
** Note: Write your answers to estimates always to one significant figure.
Image source of icon : source.
Revise and Get Paid!
If you like taking summary notes of lessons and solving past papers, see the Join Us page!